Numerical simulations have become essential in many fields to understand and solve complex problems, for example, in biology, where experiments can be long and complex to set up. Once set up, a numerical model allows to quickly test many parameters or hypotheses while having a controlled and reproducible environment. Moreover, a numerical simulation can give access to data that would otherwise be complicated to obtain because the measurement is complex or available resources are limited. In the case we are interested in, the morphogenesis of biological tissues, one of the complexities comes from the fact that many biochemical and mechanical mechanisms are involved in the process. Nevertheless, to be helpful, a numerical model must be tested and validated beforehand.

This thesis presents the model we have developed for 2D cell simulations. Unlike other types of cell models, such as "vertex models", it uses a detailed description of the cell membrane discretized into a hundred points. They follow Newtonian dynamics, with a membrane force accounting for cell deformation, an internal pressure force replacing the cell’s internal structure, and adhesion and contract pressure forces between the cells. Thus only the cell’s membrane is modeled but not the cell’s internal structures, simplifying the model description. Biological processes are either dependent on the simulated experiment, such as the cell cycle, or fixed by the model, like the cell state evolution. The latter uses the internal pressure variation by changing the cell mass to simulate a growth or apoptosis state. Since the cell cycle may depend on the diffusion of chemical species, the cell model can be coupled to an LBM model simulating this diffusion.

This model has been implemented in C++ based on the Palabos library [67], especially for managing parallelism and LBM simulations. Parallelism in Palabos is done according to a spatial domain division, so the model’s different mechanisms have been implemented to be spatially parallelized. Nevertheless, the parallelization efficiency depends strongly on the simulation’s spatial distribution of the cells. When the distribution is homogeneous, the parallelization works rather well. On the contrary, the inhomogeneous cell distribution of the threads does not have a very interesting speedup.

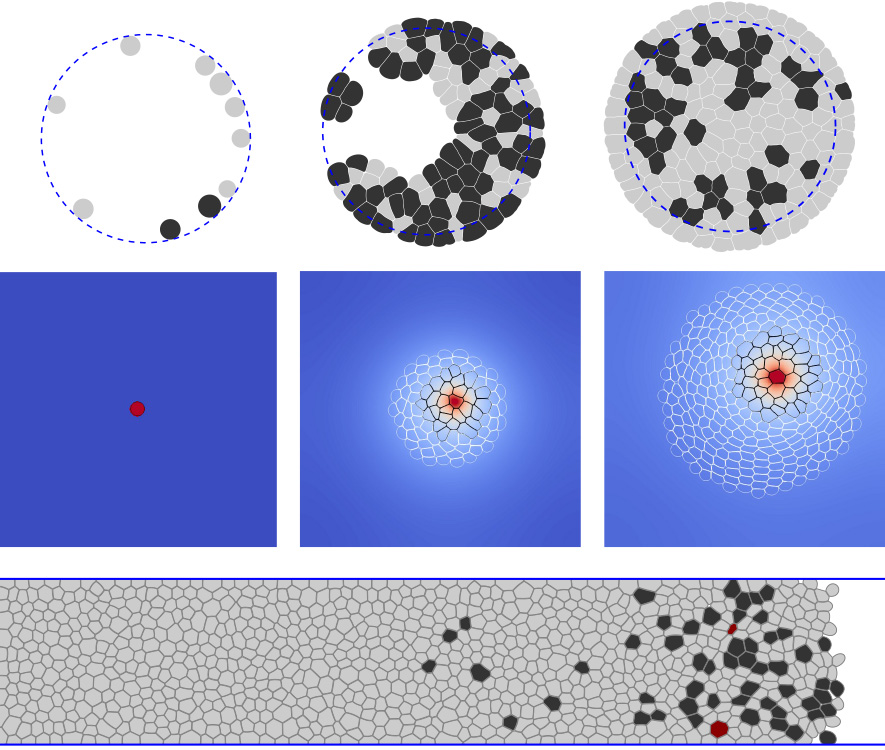
Biological validation of the model was performed in two steps; first, the single-cell properties, then the cell distribution in growing tissue. The viscoelastic-incompressible properties of a single cell were well recovered, and the neighbors’ number distribution was similar to data from biological experiments.

The model was then used to reproduce two recent biological experiments, one by Di Meglio et al. [26], the other by Gauquelin et al. [36]. The first studied the impact of the pressure exerted on the cells on their proliferation, showing that there is a maximum pressure at which cell proliferation stops abruptly. The simulations reproduce well experiment behavior using a pressure-based cell cycle. Furthermore, by testing different functions for the relationship with pressure, we find that a linear function shows the closest results to the experimental results. The second explored the tissue displacement inside a strip by comparing experiments with normal cell proliferation and blocked cell mitosis. It showed the same velocity for the cell front in both cases but a difference in the velocity profile within the strip. By adding a simple model for cell motility and the ability of cells to undergo apoptosis, the simulations captured the change in profile structure. However, they failed to recover a comparable front velocity. The latter was most likely due to the used cell motility model, which must be too simple.