Lab 1: Matlab primer for Image Processing
Stéphane Marchand-Maillet
Stephane.Marchand-Maillet@cui.unige.ch
Sviatoslav Voloshynovskiy
Sviatoslav.Voloshynovskyy@cui.unige.ch
March 13, 2002
Abstract:
This tutorial aims at getting you to a level in Matlab
programming so that you will be able to follow subsequent exercises in
the ``Advanced Image Processing'' course given at University of Geneva.
This tutorial
does not aim at being complete and is surely not the
best you may find (on the Web
for
example).
Contents
Getting started
The first thing to do is to call the Matlab environment. Depending on which
platform you are using, this can be clicking on an icon (Windows) or typing
the matlab
command in a shell (Unix, Linux, DOS). Whatever this is, you should end
up with a prompt that resembles:
< M A T L A B >
Copyright 1984-1999 The MathWorks, Inc.
Version 5.3.1.29215a (R11.1)
Oct 6 1999
To get started, type one of these: helpwin, helpdesk, or demo.
For product information, type tour or visit www.mathworks.com.
>>
You just entered the Matlab interpreter. You may now type commands and
the result will be displayed as a response, just as in any shell.
Some useful general commands are:
-
quit
exits the environment.
-
help <command>
where <command>
is a Matlab command. By itself, help
gives the list of toolboxes (packages) that are installed on your system.
-
lookfor
<something> where <something>
is what you are looking for in plain English. Actually, lookfor
searches the expression <something>
in the help pages. Try lookfor
Fourier for example.
-
pwd
and cd
allow you to navigate in the directory structure (Unix-like notation).
-
who
gives you the list of variables currently defined. whos
gives you the same list with their size.
-
clear
all clears all variables. clear
<var1 var2> clears only the variables <var1
var2>.
-
close
all close all figures. close
closes the current figure.
-
help general
extends this list of generic commands.
Online calculation and multidimensional
variables
The matlab interpreter will respond to commands you will input at the prompt.
These commands can either be ``system commands'' (eg cd)
or ``calculation commands'' (eg 1+1).
Online calculation
Type
>> 1+1
the system responds and prompts for the next command:
ans =
2
>>
(which makes worthy a CHF 1000.- investment!).
By default the result is set into a variable called
ans.
Therefore, typing whos
gives you something like
>> whos
Name Size Bytes Class
ans 1x1 8 double array
Grand total is 1 elements using 8 bytes
which is fairly explicit. If you would like the result to be stored in
some other variable
a,
say, type
>> a=1+1
a =
2
This therefore declares and sets the variable a
to 2. From now on, a
may be used for its value
>> b=a+2
b =
4
and so on. You may declare any variable, provided its name follows some
simple rules (eg, starts with a letter, no +,-,/-* signs, etc).
Anytime you type a command, Matlab outputs the result. This may be avoided
with terminating the command by a semi-colon (;). Therefore:
>> a=1;
>> b=2;
>> c=a+b
c =
3
or
>> a=1;b=2;c=a+b
c =
3
Note the difference with
>> a=1,b=2,c=a+b
a =
1
b =
2
c =
3
You now know how to create (and delete - clear)
variables. All generic operations are available in Matlab, use help
elfun (elementary functions) for a list (see
also help ops
and help specfun).
Multidimensional variables
Typing a=1
creates a scalar variable a.
Matlab generalises this principle to vector and matrices (a vector being
a matrix with one dimension set to 1). Therefore,
>> u=[1 2 3]
u =
1 2 3
>> v=[1;2;3]
v =
1
2
3
create a row (u)
and a column (v)
vector. More generally,
>> m=[1 2 3 4; 5 6 7 8; 8 9 10 11]
m =
1 2 3 4
5 6 7 8
8 9 10 11
creates a 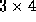 matrix.
matrix.
Provided their sizes correspond, most operations are available for matrices.
A lot of specific operations related to linear algebra are also available
and can be listed using help
matfun. Note that some operations operate on
the term level (cos,
log,
etc).
Matlab offers two other types of operations on matrices. Firstly, one may
add (or multiply) a constant value to all the matrix elements
>> m+1
ans =
2 3 4 5
6 7 8 9
9 10 11 12
Secondly, one may combine matrices globally
>> m=[1 2;3 4];
>> n=[1 0;0 1];
>> m*n
ans =
1 2
3 4
(classical matrix multiplication). Or locally
>> m.*n
ans =
1 0
0 4
(term per term multiplication). The fact of adding the ``.'' in front of
*
and /
operators makes them operate locally.
Specific commands
Matlab offers several matrix manipulation commands (see
help
elmat for a list (these include commands for
creating some specific matrices). The most basic command being the transpose
command given by '
>> m=[1 2;3 4]
m =
1 y 2
3 4
>> m'
ans =
1 3
2 4
See also help
sparfun for a list of commands operating on sparse
matrices.
Whenever it comes to creating a list, Matlab uses matrices. Matlab offers
a simple mechanism for creating some specific lists For example, the integers
between 1 and 5 are given by
>> a=1:5
a =
1 2 3 4 5
The syntax actually generalises with a step from:step:to
>> a=1:0.5:4
a =
1.0000 1.5000 2.0000 2.5000 3.0000 3.5000 4.0000
Accessing variable elements
Matlab uses parenthesis for accessing matrix (or vector) elements
>> a=2*(1:10);
>> a(5)
ans =
10
>> m=[1 2 3 4; 5 6 7 8; 8 9 10 11];
>> m(1,2)
ans =
2
(note that for matrices we have M(row,column)).
The previous mechanism gives us a technique for extracting parts of vectors
and matrices:
>> m=[1 2 3 4; 5 6 7 8; 8 9 10 11];
>> u=m(3,2:4)
u =
9 10 11
>> b=2:4;
>> x=m(3,b)
x =
9 10 11
>> v=m(:,4)
v =
4
8
11
3D arrays
Since version 5, Matlab offers the management of 3D arrays.
>> d(:,:,1)=[1 2 3;3 4 5];
>> d(:,:,2)=[2 3 4;5 2 4];
>> d(:,:,3)=[3 4 6;7 9 3];
>> d(:,:,4)=[3 6 7;2 3 5];
>> whos d
Name Size Bytes Class
d 2x3x4 192 double array
Provided sizes are consistent, matrices operations may apply on these 3D
arrays.
This is one form under which a RGB images will be stored.
Matlab programs
Matlab goes beyond this simple interaction. It offers a complete set of
programming commands that can be used to create loops, tests and other
structure any other programming language can offer (see
help
lang for a list).
Creating programs
Up to now, commands were typed one after each other within the interpretor.
Matlab offers the possibility to create batch programs (and functions)
that can be called from the interpretor (and from other batch programs).
Actually most of high-level commands of matlab correspond to batch programs.
The technique is simple:
-
create a file mycommand.m
in the current directory
-
type commands in this file
-
execute these commands by typing mycommand
in the interpretor.
Example:
Write these lines in the mycommand.m
file:
% this is my first Matlab program
a=1;
b=3;
c=a+b;
fprintf(1,'c is now %d\n',c);
and type mycommand
>> mycommand
c is now 4
The detail of commands in the mycommand.m
file can be found via the help facility. One thing to note is that anything
after a percent (%)
is a comment.
One may also create functions in a similar way. Type this in the
myfunction.m
file
function [result]=myfunction(a)
% [result]=addtwo(a)
% adds 2 to the input
% this is my first Matlab function
result=a+2;
and try
>> b=myfunction(3)
b =
5
Here, it is important that the function has the same name as its file.
One nice feature is that this permits online help, created by the first
comments in the function file.
>> help myfunction
[result]=addtwo(a)
adds 2 to the input
this is my first Matlab function
From then on, one can build a complete library (toolbox) of functions with
the appropriate documentation. Simply put all function files in a directory
dir,
add its path on the search path (with addpath('dir')).
help
dir will then display the first comments of each
M-file. Any toolbox is done like this (try which
logm) to see the file corresponding to the logm
command.
Programming instructions
On top of calculations commands, Matlab proposes generic programming instruction
for creating loops, test and so on.
if
test
if I == J
A(I,J) = 2;
elseif abs(I-J) == 1
A(I,J) = -1;
else
A(I,J) = 0;
end
Note: The NOT condition is given by the tilde (~=, not
equal).
for
loop
for I = 1:N,
for J = 1:N,
A(I,J) = 1/(I+J-1);
end
end
Note that instead of 1:N
we could have any integer row vector.
while
loop
E = 0*A; F = E + eye(size(E)); N = 1;
while norm(E+F-E,1) > 0,
E = E + F;
F = A*F/N;
N = N + 1;
end
switch
test
switch lower(METHOD)
case {'linear','bilinear'}
disp('Method is linear')
case 'cubic'
disp('Method is cubic')
case 'nearest'
disp('Method is nearest')
otherwise
disp('Unknown method.')
end
See help lang
for further instructions.
Some useful commands and tips
Commands
When manipulating matrices and images, the following commands are often
very useful (see their respective help).
-
length
returns the largest dimension of an array.
-
size
returns the dimension of an array
-
sum
sums the element of an array along its first non-singleton dimension (columns
for a matrix)
-
max
returns the largest element of an array along its first non-singleton dimension
(columns for a matrix)
-
min
returns the smallest element of an array along its first non-singleton
dimension (columns for a matrix)
-
rand
generates random numbers
-
sort
sorts numbers
-
conv2
operates a 2D convolution between a matrix and a mask
-
imread
reads an image in a given format as a matrix
-
imwrite
write a matrix as an image
-
fft2,
dct2
2D- Fourier and DCT transform of an array.
Tips
-
Have explicit names for variables
-
When creating a matrix, declare it first as a complete array rather
than element by element. Compare:
clear m;
for i=1:500
for j=1:500
m(i,j)=i+j;
end
end
and
clear m;
m=zeros(500);
for i=1:500
for j=1:500
m(i,j)=i+j;
end
end
Use global operations rather than local, ie
u=1:500;
v=u.*(u>500);
rather than
u=1:500;
for i=1:500
if u(i)>500
v(i)=u(i);
else
v(i)=0;
end
end
use [value index]=sort(rand(1,n))
to generate a random selection within the set of the first n
integers.
Exercises
-
Test whether a given matrix is symmetric, orthogonal, singular or otherwise.
-
Load an image and save it after a rotation of 90 degrees.
-
Load an image and calculate its RGB histograms (in at least two different
ways).
-
Imagine what you can do with Matlab :o)
MARCHAND-MAILLET stephane
Mon Mar 12 12:10:06 MET 2001